Imaginary unit
Imaginary unit: brief history
Does every quadratic equation have a real solution?
This is the first question, where a fresh concept or a new branch of mathematics has started. Yes, it's the story behind complex analysis or complex numbers or imaginary numbers.
The equation behind this brand new concept is:
The problem was to find the roots of this equation. As we all know that, one of the main features of a real number is it's square is always positive. Here, the problem started when mathematicians tried to find the root of a negative real number. i.e. x=√(-1) =???
This is the scene when the concept of complex numbers and imaginary unit begins.
The square root of (-1) becomes an icon and mathematicians represented it uniquely by the symbol "i". i.e. i=√-1.
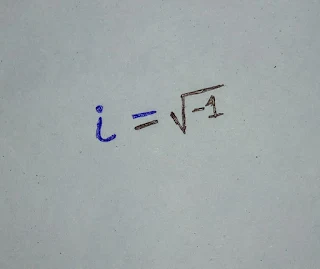 |
Again, since every number has two possible square roots: one positive and one negative; (-1) demands a negative square root also. This idea introduces "-i". i.e. , -i=-√-1.
This is the brief history of imaginary unit.

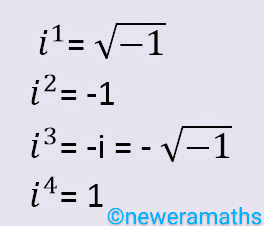
No comments:
Post a Comment